Menu
 

Introduction :

La technologie RSA est protégée par un brevet dans certains pays (aux Etats-Unis, ce brevet expira en septembre 2000 ; en France il n’y a pas de brevet). Elle a été commercialisé par plus de 350 entreprises, et l’on estime que plus de 300 millions de programmes installés utilisent le RSA ; votre ordinateur contient sans doute de tels programmes, qui sont activés – sans même que vous le sachiez – lorsque, par exemple, vous souhaitez mener des transactions sécurisées sur L’internet.
Le RSA est inclus dans de nombreux standards informatiques, dont le Society for Worldwide Interbank Financial Telecommunication Standart ou le French Financial Industry’s ETEBAC-5 Standart, ou encore le X9.44 draft Standart for the U.S. Banking Industry. Le RSA est programmé aussi dans les systèmes d’exploitation de Microsoft, d’Apple, de Sun et de Novel. Il est intégré dans les cartes Ethernet et dans certaines cartes à puce bancaire. Un très grand nombre d’institutions gouvernementales, universitaires ou militaires l’utilisent de façon interne. Le réseau Internet en fait un usage systématique pour assurer la confidentialité du courrier électronique et authentifier les utilisateurs. Bref, le RSA est partout.

Le protocole RSA se fonde sur le théorème suivant :

Soient p et q deux nombres premiers.
On pose n = p q.
Si le nombre e est un entier premier avec le nombre (p – 1) (q – 1), alors il existe un unique entier d positif, tel que
1< d< (p-1)(q-1)   et vérifiant   e d ≡ 1 [(p-1)(q-1)],
et, pour cet entier d et un entier A quelconque, on a :
Aed ≡ A [n]

Démonstration :

1) Montrons que si e, tel que 1<e<(p-1)(q-1), est premier avec le produit (q-1)(p-1) alors il existe d unique tel que 1<d<(p-1)(q-1) et vérifiant e d ≡ 1 [(p-1)(q-1)]

Si eÙ(p-1)(q-1)=1, il existe d’après le théorème de Bézout, deux entiers relatifs u et v tels que :
                                                              u (p-1)(q-1) + v e = 1
on peut définir 2 autres entiers u' et v' tels que
                                                              u (p-1)(q-1) + v e = u' (p-1)(q-1) + v' e = 1
nous avons par conséquent :             (u' -u)(p-1)(q-1) = - (v'- v) e
Il existe donc un entier k tel  que             u'=u+k e    et    v' = v - k (p-1)(q-1)

D’après la division euclidienne, nous avons donc  0£v<(p-1) (q-1)

D’après Bézout, nous avons  u (p-1)(q-1) = 1 – v e  (division de u (p-1)(q-1) par –e  donc 1<v)  soit  v e ≡ 1 [(p-1)(q-1)]
Nous avons donc d = v.

Montrons que d est unique
Supposons qu’il en existe un autre, nous avons donc e(d-d')≡0 [(p-1) (q-1)]
Comme e est premier avec (p-1)(q-1) alors (d-d')≡0 [(p-1)(q-1)]. Mais comme on a 1<d'<(p-1)(q-1) et 1<d<(p-1)(q-1) alors d=d'.

2) Par hypothèse e est premier avec (p – 1)(q – 1). D’après l’identité de Bézout, il existe (d, f) dans ℕ ´ ℤ tel que 
d e + f (p –1) (q – 1) = 1  soit    f (p – 1) (q – 1 ) = 1 – d e

Donc il existe d Î ℕ tel que  d e – 1 soit divisible par (p – 1) (q – 1).
Soit C≡Ae[n], donc C - Ae est un multiple de n. De plus comme Cd – Aed = (C – Ae ) (Cd - 1 + Ae Cd - 2 +...+ Aed - 2C + Aed - 1), Cd – Aed  est aussi un multiple de n.


Si A n’est divisible ni par p ni par q, alors, d’après le petit théorème de Fermat, p et q divisent respectivement Ap – 1 – 1 et Aq – 1 – 1. Donc p et q divisent  A(p - 1)(q - 1) – 1 car cet entier est multiple de Aq - 1 – 1 et Ap - 1 – 1.  (  A(p - 1)(q - 1) – 1= (Ap – 1 –1 )( 1 + Ap – 1 + A2( p – 1) +...+ A(q – 2)(p – 1)) )

Or d e – 1 est divisible par (p – 1) (q – 1 ), il existe donc kÎ ℕ* tel que d e – 1 = k (p – 1) (q – 1).
Ainsi on a Aed - A = A1 + k(p - 1)(q - 1) – A = A(Ak(p - 1)(q - 1) - 1) = A(A(p - 1)(q - 1) – 1 )(A(k - 1)(p - 1)(q - 1) +...+ 1).

Donc Aed - A est divisible par n = pq.


Comme Cd - A = (Cd – Aed) + (Aed – A ), Cd - A est divisible par n. Donc Cd ≡ A[n], donc Aed ≡ A[n]

Méthode de fonctionnement du système RSA :

La méthode de cryptographie RSA a été inventée en 1977 par Ron Rivest, Adi Shamir et Len Adleman, à la suite de la découverte de la cryptographie à clé publique par Diffie et Hellman. Le RSA est encore le système cryptographique à clé publique le plus utilisé de nos jours. Il est intéressant de remarquer que son invention est fortuite : au départ, Rivest, Shamir et Adleman voulaient prouver que tout système à clé publique possède une faille.

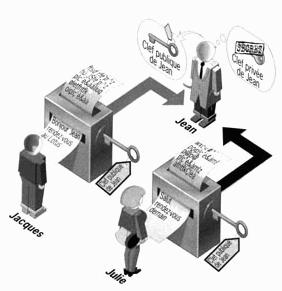
Principe de fonctionnement : Si Jean souhaite recevoir des messages en utilisant le RSA, il procède de la façon suivante :

Création des clés : Jean crée 4 nombres p,q, e et d :

  • p et q sont deux grands nombres premiers distincts. Leur génération se fait au hasard, en utilisant un algorithme de test de primalité probabiliste.
  •  e est un entier premier avec le produit (p-1)(q-1).
  • d est tel que ed=1 modulo (p-1)(q-1). Autrement dit, ed-1 est un multiple de (p-1)(q-1). On peut fabriquer d à partir de e, p et q, en utilisant l'algorithme d'Euclide.
  • on a n = pq.

Distribution des clés :

Le couple (n,e) constitue la clé publique de Jean. Il la rend disponible par exemple en la mettant dans un annuaire. Le couple (n,d) constitue sa clé privée. Il la garde secrète.

Envoi du message codé :

Julie veut envoyer un message codé à Jean. Elle le représente sous la forme d'un ou plusieurs entiers M compris entre 0 et n-1. Julie possède la clé publique (n,e) de Jean. Elle calcule C=Me mod n. C'est ce dernier nombre qu'elle envoie à Jean.

Réception du message codé :

Jean reçoit C, et il calcule grâce à sa clé privée D=Cd (mod n). D'après un théorème du mathématicien Euler, D=Mde =M (mod n). Il a donc reconstitué le message initial.

Intérêt de la méthode :

Tout l'intérêt du système RSA repose sur le fait qu'à l'heure actuelle il est pratiquement impossible de retrouver dans un temps raisonnable p et q à partir de n si celui-ci est très grand (ou alors, si c'est possible, les cryptanalystes qui ont trouvé la méthode la gardent secrète). Alice est donc la seule à pouvoir calculer d dans un temps court. De plus, elle n'a jamais à transmettre les entiers p et q, ce qui empêche leur piratage.

 

 

Programme encodé sous maple permettant de crypter et de décrypter un message selon le système RSA

Exemple :

·         Chiffrement :

Jean veut donc envoyer un message à Julie. Il cherche dans l'annuaire la clef de chiffrement qu'elle a publiée. Il sait maintenant qu'il doit utiliser le système RSA avec les deux entiers n et e (prenons par exemple n=5141=53·97 et e=7, premier avec 52·96=4992). Il transforme en nombres son message en remplaçant par exemple chaque lettre par son rang dans l'alphabet.

"JEVOUSAIME" devient : "10 05 22 15 21 19 01 09 13 05".

Puis il découpe son message chiffré en blocs de même longueur représentant chacun un nombre plus petit que n. Cette opération est essentielle, car si on ne faisait pas des blocs assez longs (par exemple si on laissait des blocs de 2 dans notre exemple), on retomberait sur un simple chiffre de substitution que l'on pourrait attaquer par l'analyse des fréquences.

Son message devient : "010 052 215 211 901 091 305"
Un bloc B est chiffré par la formule C = Be mod n, où C est un bloc du message chiffré que Jean enverra à Julie.
 Après avoir chiffré chaque bloc, le message chiffré s'écrit : "0755 1324 2823 3550 3763 2237 2052"

·         Déchiffrement :

Julie calcule à partir de p et q, qu'elle a gardés secrets, la clef d de déchiffrage (c'est sa clef privée). Celle-ci doit satisfaire l'équation e·d mod ((p-1)(q-1)) = 1. Ici, d=4279.
Chacun des blocs C du message chiffré sera déchiffré par la formule B = Cd mod n.

Elle retrouve : "010 052 215 211 901 091 305"

           Accueil